Astrology Charts Are Not Flat

Astrology charts are now calculated with the convenience of a computer, but this only shows us 2 of the 3 dimensions. The chart can look very different when we take into account declination, latitude, right ascension, true-body aspects and other 3-dimensional factors.

How We Do Astrology

Most astrologers now use a computer to calculate charts; and as time passes, fewer and fewer of us have ever calculated a chart by hand. The computer is a great boon, it stops us making errors in the calculations, it calculates a chart almost instantly, but it removes us from the details. Consequently, many astrologers no longer have an instinctive feel for what is happening in the sky, for what a chart represents in terms of what we would see if we went outside and looked up at the sky. Astrology started outdoors with people looking at the sky. When it moved indoors, when people started drawing charts to represent the positions of the planets rather than looking at what was happening in the sky, we slowly began to lose touch with the sky.

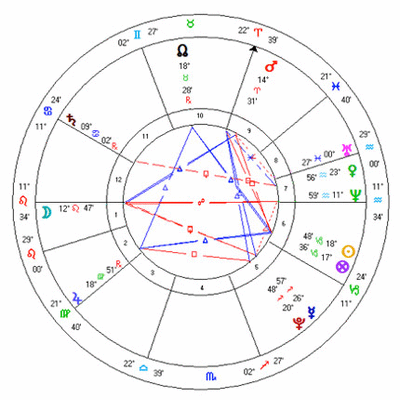
A standard astrological chart, such as the one shown in figure 1, gives considerable information, but it misses much. It shows each planet's position in the zodiac, known technically as the planet's ecliptic longitude, but that is just one dimension. The chart only shows a planet's distance from zero Aries, a flat one-dimensional view, but charts are not flat, and there is much more to a chart than just this one distance. I will use this chart as an example later, but for now look at the Moon and think what its position relative to the ascendant might mean.

This article is not intended to say how we should do astrology; it is not proposing answers to questions about the implications of charts not being flat, rather it is raising questions that astrologers should be aware of and should think about. It is intended to make the questions clear and, I hope, provide information so that readers can understand the issues and make up their own mind. If there is more than one way of doing astrology, more than one understanding of the relationship between planets, we should chose the method we use for a reason, and after having thought about it, rather than because we have always done it that way. Understanding the issues is how our astrological practice develops.

I have excluded mathematics from the article. The appendix included references to technical information, and, for those who wish to understand the mathematical detail and who have an understanding of trigonometry, some more mathematical sources. Note: everything I cover can be understood without mathematics!

The Earth and the Sky

We need to start with figure 2 which shows a simple diagram of the Earth. As it rotates on its axis, the Earth turns from west to east. Now, imagine that you are the Sun shining down on the Earth.

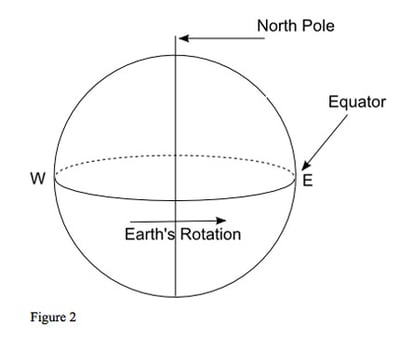
First you are shining on the Far East; then, as the Earth turns, on Europe, then the Atlantic Ocean, then on the Americas. This simple rotation is the basis of the hour-by-hour changes in an astrological chart: the movement of the angles through the signs and the change in the house position of each planet; but to understand what is happening, we need to change our point of view from the Earth to the sky.

Now consider the diagram of the Earth and the celestial sphere shown in figure 3. The celestial sphere is just the projection of the Earth into the sky. In particular, the Earth's equator is projected outwards onto the sky to become the celestial equator, which rotates with the Earth's equator as the Earth turns. If we look at the sky from somewhere on Earth, we see the Sun appear to move across the sky, rise in the east, culminate in the south (if we are in the northern hemisphere) and set in the west. It is as if the celestial sphere turned from east to west.

In the physical world, the Earth turns from west to east. This makes it look as if the sky, and all the planets and stars, are moving from east to west. It does not matter which of these two ways we chose to look at things, but for our purposes it is easier to think of the Earth as fixed and the sky rotating around us. This is what we see when we look up into the sky.

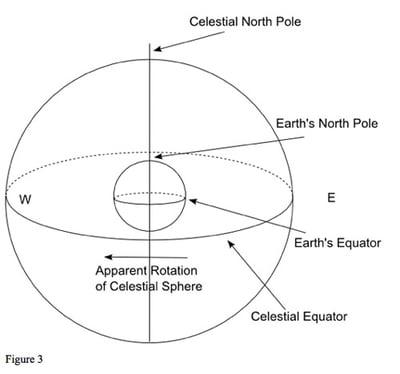
An astrological object, such as a planet or a star, has a position on the rotating celestial sphere given by two coordinates. Rather like specifying the position of a city on Earth by its geographic latitude and longitude, we can specify a position in the sky with reference to the celestial equator. However, there is also another way of specifying a position, and to understand it we need to think about the Earth's orbit around the Sun.

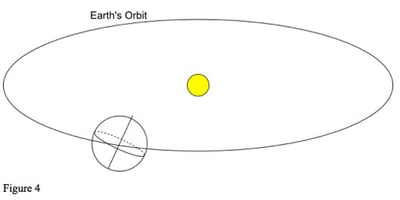
In figure 4, (the diagram is not to scale!) the Earth is shown with its axis correctly tilted. This tilt gives us the changing seasons, summer and winter. The axis always points in the same direction, north. (The Earth's North Pole points towards the Pole Star.) The Earth's orbit around the Sun defines the ecliptic. If we project the orbit onto the sky, it gives the apparent path of the Sun through the year. As the other planets have orbits round the Sun that are in almost the same plane as the Earth's, the same flat disc, they are always close to the ecliptic, as seen from Earth. (The exception being Pluto, which can be over 17 degrees from the ecliptic). We can see that the Earth's equator and the ecliptic are at an angle to each other. The two points where they cross are zero Aries and zero Libra. A planet, such as the Sun, moving along the ecliptic in its normal direct motion will move from south of the equator to north of the equator at zero Aries, and from north of the equator to south at zero Libra: see figure 5.

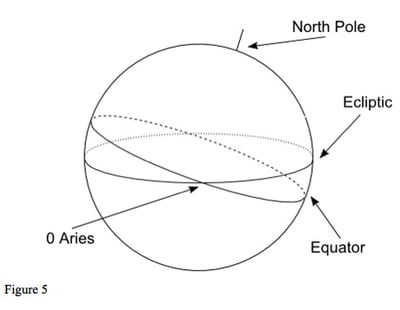
Ecliptic and Equatorial Positions

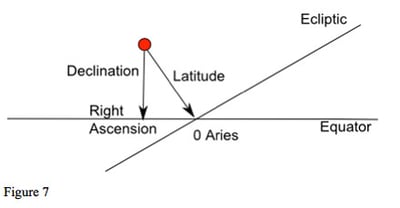
Before moving on to what all this looks like for an observer on Earth, we should think about how we might specify the position of an object in the sky. We can define a position with reference to either the ecliptic or the equator. If we use the ecliptic then, like longitude and latitude on earth, the position of a planet along the ecliptic is called celestial longitude (or just longitude). This is our normal zodiac position of the planet, the position used in astrological charts. The distance of the planet from the ecliptic is called its celestial latitude (or just latitude); see figures 6 and 7.

We can also define a position with reference to the celestial equator. If we also used the terms latitude and longitude for this, things would get very confused! Instead, we use right ascension for the distance along the equator measured from where the equator and ecliptic cross (zero Aries) and we use declination for the distance from the celestial equator. Many astrologers will be familiar with the term declination but perhaps not realise what it means.

Although declination, like latitude, is measured in degrees, right ascension is not; it is measured in time, in hours and minutes. This seems rather strange until we remember that the earth rotates on its axis at a constant rate, and so the celestial equator seems to rotate at a constant rate for an observer on earth. It takes 24 hours to rotate 360 degrees: the circle of 360 degrees is equivalent to 24 hours of right ascension. We will see later that right ascension and declination are used in determining the rising and setting times of planets.

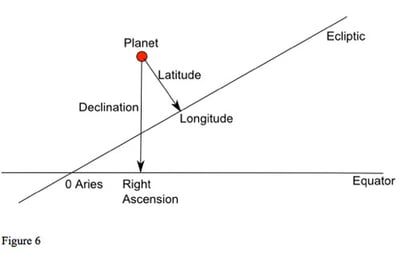
Because the ecliptic and equator are at an angle to each other (because of the tilt of the earth's axis), longitude and right ascension are not equal, as we can see from figure 6. Even if a planet is at zero Aries, but has non-zero latitude, it will not be at zero right ascension, as shown in figure 7.

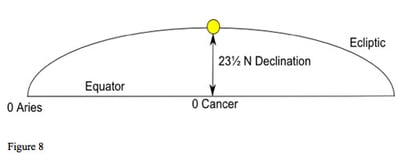
The Sun is the only planet that is always on the ecliptic, so always has zero latitude. The other planets are close to, but not exactly on, the ecliptic and so have latitude. As the Sun moves from zero Aries at the spring equinox, through Taurus and Gemini to come to zero Cancer at the summer solstice, it moves to increasing northern declination as the ecliptic here is north of the equator (figure 8). At the solstice, it will be at 23½ degrees north declination, but still exactly on the ecliptic with zero latitude. From zero Libra, through Capricorn to zero Aries, it will have southern declination.

The important point is that there are two different ways of measuring position; they are both valid and are used for different purposes. This is a good point to discuss our first example of the practical effects of a chart not being flat: the effect on aspects.

How Do We Measure Aspects?

In an astrological chart, such as that in figure 1 above, we measure aspects as the difference in ecliptic longitude between two bodies, but once we take into account the second dimension, the ecliptic latitude, various questions need to be asked.

The simplest case is the conjunction. Two planets are in conjunction, with a certain orb, when they are close in longitude, and we measure the orb by the difference in their longitude. In figure 9, we have a conjunction of two planets with an orb of 40 minutes: 6TA30 to 7TA10. However, one is 2 degrees 15 minutes north of the ecliptic and the other 0 degrees 45 minutes south. They are 3 degrees apart in latitude. Does this affect the conjunction, and if so, how?

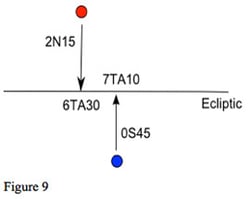
Now suppose that we have a wider conjunction, as shown in figure 10, with an orb of 2 degrees, but with both planets on the ecliptic. How does this compare with the closer conjunction, measured on the ecliptic, but with a significant difference in latitude? Should we just look at the orb along the ecliptic, or perhaps the actual angular separation of the two planets is what matters.

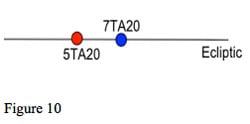
Opinions on the effect of latitude on aspects vary. Some astrologers take the view that the ecliptic positions are all that we need to consider, others that the actual distance, the 'true-body' aspect is what matters. Others look mainly at the ecliptic distance, but consider the conjunction stronger if the two planets are close in latitude.

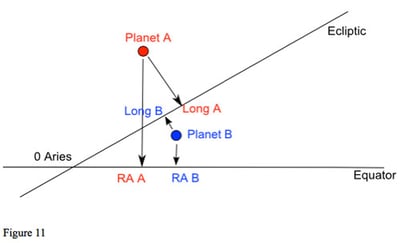
Another issue is shown in figure 11. Assume that Planet A is moving faster than Planet B and that we are near the conjunction. If we consider their zodiac longitude, Planet A has passed Planet B: the conjunction is separating. However, if we look at the positions on the equator and consider their right ascension, Planet A is applying to Planet B. If we consider the actual distance between the two planets, they are about as close to each other as they will get, Planet A is at its true-body closest approach to Planet B. Once we allow other viewpoints and do not just look at zodiac longitude, we find that even a simple question of whether an aspect is applying or separating may not be as simple as it seems.

Finally, we should note that the fixed stars are distributed all over the celestial sphere, some with very large latitudes and declinations. To say that a planet is conjunct a particular fixed star can involve a very large difference in latitude. Does it matter?

As with all these questions, there are no right or wrong answers on offer, just issues to consider.

Longitude and Declination

Many people use two dimensions in astrology, the zodiac longitude and the declination, treating planets with the same declination as if they are in conjunction. However, we have seen that longitude goes with latitude, as both are based on the ecliptic, but right ascension goes with declination as both are based on the equator. So why do we mix the two measurements? The reason not only makes sense, but also explains why we treat planets with the same declination as being in conjunction. However, before we can discuss how we use declination, we need to look at one more reference plane: the horizon (which, amongst other things, defines the position of the ascendant and the rising and setting times of planets).

The Horizon

In figure 12, we have our familiar diagram of the earth showing the equator and ecliptic. We also have an observer (at about 40 degrees north geographic latitude).

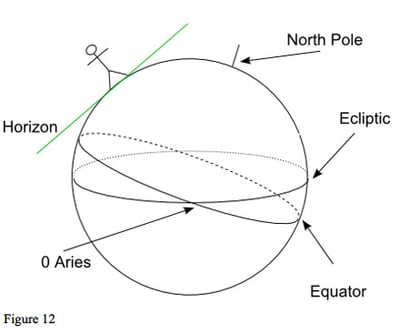
The observer's horizon defines his viewpoint when he looks at the sky: which planets have risen above the horizon, and which are below. We usually think of the horizon as being level, stretching out in all directions from us, not tilted. Figure 13 shows the earth as we experience it: the horizon level and the ecliptic and equator at an angle to it.

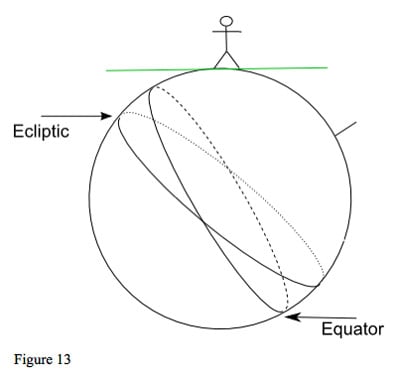
The closer an observer is to the geographic equator, the higher in the sky the celestial equator and the ecliptic will appear. As the Sun is always on the ecliptic, it will be high in the sky at noon for an observer near the equator, but if the observer is near the North Pole, the Sun will appear lower down.

We can now take figure 13 and project it onto the celestial sphere, so the horizon is in the centre of our diagram. This gives us figure 14, which looks rather complicated, but is really just a slight development of what we have seen before. We have the horizon with the celestial equator passing through the points East and West of the observer, and being at its maximum elevation above the horizon in the south. The ecliptic is shown in red with zero Aries currently just north of east and below the horizon.

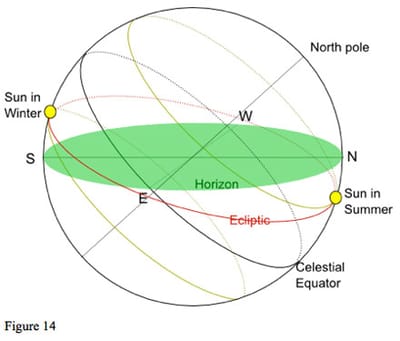
Two possible positions of the Sun are shown. On the left, the Sun (always on the ecliptic) is at zero Capricorn, and so south of the equator at 23½ degrees south declination. As the Earth turns, the Sun will trace-out the path round the celestial sphere shown in yellow. Note that it will spend more time below the horizon than above; the days will be shorter than the nights. (In order to make the effect of declination clear, the diagram has been exaggerated.)

If we now look at the right of figure 14, we have the Sun at zero Cancer and so 23½ degrees north of the celestial equator, 23½ degrees north declination. This time, as the earth turns, the Sun will trace-out a path round the celestial sphere that spends more time above the horizon than below: the days are longer than the nights.

Parallels in Declination

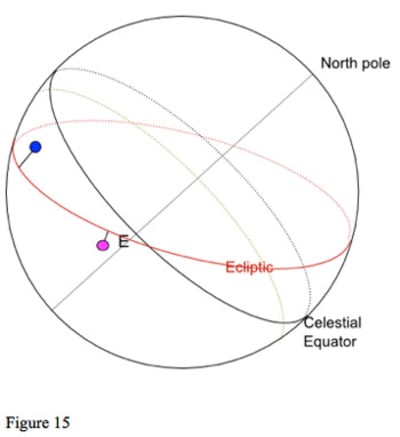
Suppose we have two planets with the same declination, that are not on the ecliptic and do not have the same latitude as in figure 15. The planet shown in blue is north of the ecliptic, the planet shown in purple is south of the ecliptic. There is no particular relationship between their zodiac longitude positions; however, the two planets are the same distance south of the equator: they have the same declination.

As we see in figure 16, as the earth turns the two planets will follow the same circle of declination round the celestial sphere (called a diurnal circle). The two planets will pass through the same positions relative to the horizon as seen from the Earth. They will rise at the same position on the horizon (at different times); they will set at the same position on the horizon, and they will rise to the same altitude above the horizon in the south.

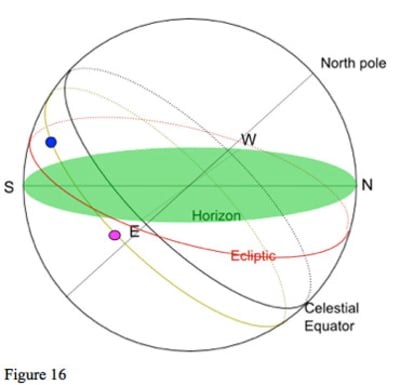
If, from a particular location, one of the planets seems to pass just above the top branches of a particular tree, then some time later the other planet will pass just above the top of that tree. It is as if they are the same planet but a number of hours apart. This may be why they seem to have the same effect, as if they were in conjunction.

Conjunctions in longitude and parallels in declination derive from the two fundamental rotations in astrology. A parallel in declination relates to what happens as the Earth turns on its axis, a conjunction in longitude relates to what happens as planets move in their orbits around the Sun.

The Ascendant

The horizon defines the position of the Ascendant: where the ecliptic intersects the horizon in the east. Let us return to the chart shown as figure 1 at the start of this article.

The Ascendant, at 11 Leo 34, is where the ecliptic intersects the horizon, the point of the ecliptic rising as shown in figure 17. The ecliptic position of the Moon, at 12 Leo 47 has not yet risen, but the Moon has northern latitude, and is 5 degrees 2 minutes north of the ecliptic. The body of the Moon has already risen above the horizon. If we went outside and looked at the sky very low down in the east, we would see the Moon 2 degrees 14 minutes above the horizon.

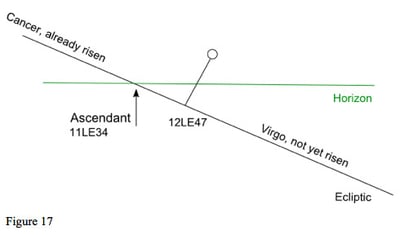
So, how do we interpret this Moon? The chart shows it as a first house Moon, but bodily it is a twelfth house moon. The latitude, the second dimension of the chart does not just affect aspects, as we discussed above, but can have an effect on the question of a planet's house, and so on its interpretation.

Looking again at the chart in figure 1 we see Neptune on the Descendant. Its zodiac position is in the seventh house 25 minutes from the Descendant, and because it is almost exactly on the ecliptic (just 2 minutes south latitude) its bodily position is also in the seventh, it is 18 minutes above the horizon. If a planet has no latitude (or very little), there is no distortion.

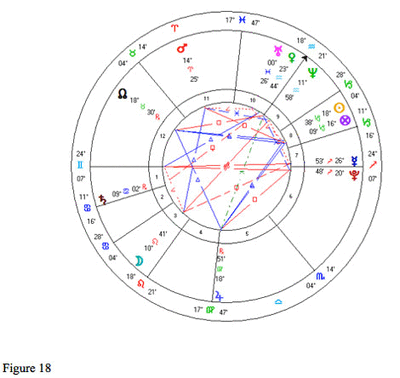
It is worth seeing just how large the distortion can become. If we set the chart in figure 1 for four hours earlier, at 14:10, we have Mercury and Pluto setting: figure 18. Here it looks like Pluto has set and Mercury is about to set, Pluto in the sixth house and Mercury in the seventh. Mercury is indeed 3 degrees 39 minutes above the horizon, but Pluto is nearly 6 degrees above the horizon; it is higher in the sky than Mercury. Although it looks from the chart as if Pluto is in the sixth house, it will not set bodily for another 43 minutes at 14:53 with the descendant at 4 Capricorn 07 when Pluto's zodiac position will be just over 13 degrees into the sixth house below the horizon.

Is the ecliptic position of a planet what matters, or is its bodily placement above or below the horizon what is important?

Declination and Right Ascension ~ Planets Rising and Setting

The rising and setting of planets is determined by their declination and right ascension. If a planet has northern declination then (in the northern hemisphere) it will spend more time above the horizon than below, and the further north of the equator it is, the longer it will be above the horizon. Some fixed stars with large declination never set. The exact relationship involves some mathematics, but a few examples are interesting.

At the geographic latitude of London, a body with declination greater than 38N30 will never set. It will be what is known as 'circumpolar'. Figure 19 shown a long exposure of the northern sky (courtesy LCGS Russ, October 1982) showing circumpolar stars with high northern declination.

The time at which a planet or star rises and sets will depend on its right ascension, and from the body's declination and right ascension, and the location of the observer it is straightforward (using advanced mathematics) to calculate exactly when it will rise and set. What we see in the sky in terms of which bodies are above or below the horizon depends not just on one dimension, but on two.

House Positions and Chart Representation

The discussion of house positions, above, focused on planets rising and setting. A discussion of the intermediate house cusps, the different house systems, and the house position of a planet taking into account its latitude is far too long a topic for this article. However, I hope it has become clear that how we view a chart, and how we interpret it, can be significantly affected by planetary latitude. Such seemingly simple questions as, is a planet in the first or twelfth house, may not be as simple as we may think.

All this leads on to a consideration of how we should draw a chart to show these 'off-ecliptic' positions? Do we need a new form of chart? Like a discussion of house systems, new ways of drawing charts involves a much longer discussion than there is space for here. However, if we want to recapture something of the original outdoor astrology, the astrology that observed the planets in the sky and noted their bodily placements, not just their ecliptic positions, we may find that we need to find new ways of representing charts. Perhaps modern computer graphics can change the way we understand the heavens, and even the way we do our astrology. We will see!

Appendix